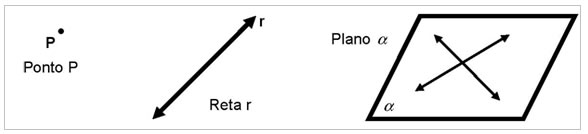
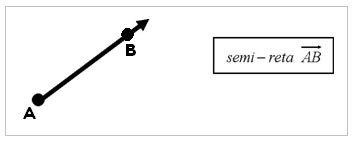
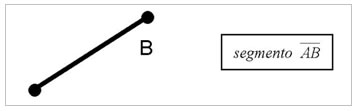
2) ÂNGULOS
2.1)REGIÃO CONVEXA : Uma região é convexa se, se somente se, o segmento determinado por dois pontos quaisquer dessa região estiver contido nela. |
|
2.3) ÂNGULOS
A união de duas semi-retas distintas não opostas de mesma origem chamamos ângulo. Considere as semi-retas PA e PB não colineares da figura. O conjunto
união dessas duas semi-retas é chamado ângulo. As semi-retas PA e PB são chamadas lados desse ângulo. O ponto P é chamado vértice desse ângulo. |
|
2.3.1) EXTERIOR E INTERIOR DE UM ÂNGULO
Dois semi-planos abertos (semi-plano menos a reta que é a origem) determinados pelas retas que contém os lados do ângulo, considere aqueles que não contém pontos do ângulo. O conjunto união desses dois semi-planos é chamado exterior do ângulo. O conjunto complementar, em relação ao plano do ângulo, da união desse ângulo com seu exterior é chamado interior do ângulo. |
|
2.3.2) SEMI-RETA INTERNA A UM ÂNGULO
Uma semi-reta é interna a um ângulo quando tem origem no vértice do ângulo e pontos internos do ângulo pertencem a ele |
|
2.3.3) ÂNGULOS CONSECUTIVOS Dois ângulos são consecutivos quando têm o mesmo vértice e têm um lado em comum. |
|
A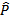 B e B B e B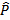 C são consecutivos (têm o lado PB comum). Note que neste caso eles têm apenas os pontos de um lado comum. R C são consecutivos (têm o lado PB comum). Note que neste caso eles têm apenas os pontos de um lado comum. R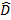 T e R T e R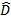 S são consecutivos (têm o lado RD comum). Note que neste caso eles têm também pontos internos em comum. S são consecutivos (têm o lado RD comum). Note que neste caso eles têm também pontos internos em comum.
|
2.3.4) ÂNGULOS ADJACENTES
Dois ângulos são chamados adjacentes se são consecutivos e não têm pontos internos em comum. |
|
A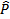 B e B B e B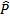 C são adjacentes. A C são adjacentes. A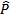 B e A B e A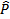 C são consecutivos e não são adjacentes. C são consecutivos e não são adjacentes.
|
2.3.5) ÂNGULOS CONGRUENTES
Dois ângulos são congruentes se, e somente se, têm a mesma medida.
|
2.3.5) ÂNGULOS CONGRUENTES
Dois ângulos são congruentes se, e somente se, têm a mesma medida.
2.3.6) BISSETRIZ DE UM ÂNGULO É uma semi-reta interna a esse ângulo que o divide em duas partes iguais. |
|
2.3.7) ÂNGULO RETO É o ângulo que tem a sua medida valendo 90º e sua representação é dada por duas semi-retas perpendiculares.
|
|
2.3.8) ÂNGULO AGUDO E OBTUSO
Se um ângulo não nulo for menor que um ângulo reto, ele é chamado ângulo agudo e se um ângulo não raso (180º ) for maior que um ângulo reto ele é chamado ângulo obtuso. |
|
2.3.9) ÂNGULOS COMPLEMENTARES, SUPLEMENTARES E REPLEMENTARES
Dois ângulos são complementares quando a soma de suas medidas for 90º. Cada um deles é chamado complemento do outro.
Dois ângulos são suplementares quando a soma de suas medidas for 180º. Cada um deles é chamado suplemento do outro.Dois ângulos são replementares quando a soma de suas medidas for 360º. Cada um deles é chamado replemento do outro.
2.3.10) ÂNGULOS NULO, COMPLETO, RASO E RETO
Ângulo nulo é aquele que tem medida igual a 0º. Ângulo completo é aquele que tem medida igual a 360º. Ângulo raso é aquele que tem medida igual a 180º . Ângulo reto é aquele que tem medida igual a 90º .
2.3.11) ÂNGULOS OPOSTOS PELO
É um par de ângulos formados por duas retas concorrentes e por sua vez , possuem a mesma medida.
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|