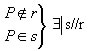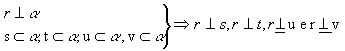Geometria Espacial
Conceitos primitivos
São conceitos primitivos ( e, portanto, aceitos sem definição) na Geometria espacial os conceitos de ponto, reta e plano. Habitualmente, usamos a seguinte notação:
- pontos: letras maiúsculas do nosso alfabeto
|
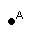 |
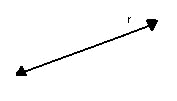
- retas: letras minúsculas do nosso alfabeto
|
|
- planos: letras minúsculas do alfabeto grego
|
|
Observação: Espaço é o conjunto de todos os pontos.
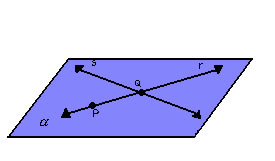
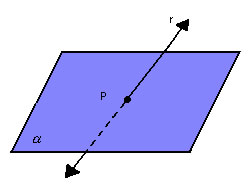
Por exemplo, da figura a seguir, podemos escrever:
|
|
Axiomas
Axiomas, ou postulados (P), são proposições aceitas como verdadeiras sem demonstração e que servem de base para o desenvolvimento de uma teoria.
Temos como axioma fundamental:existem infinitos pontos, retas e planos.
Postulados sobre pontos e retas
P1)A reta é infinita, ou seja, contém infinitos pontos. |
 |
P2)Por um ponto podem ser traçadas infinitas retas. |
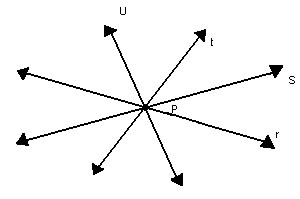 |
P3) Por dois pontos distintos passa uma única reta. |
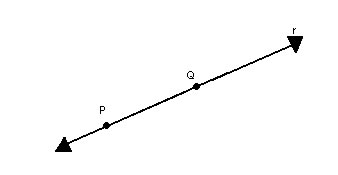 |
P4) Um ponto qualquer de uma reta divide-a em duas semi-retas. |
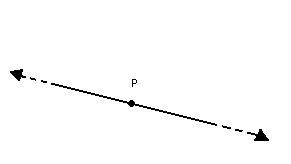 |
Postulados sobre o plano e o espaço
P5) Por três pontos não-colineares passa um único plano. |
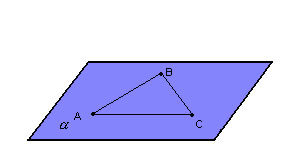 |
P6) O plano é infinito, isto é, ilimitado.
P7) Por uma reta pode ser traçada uma infinidade de planos. |
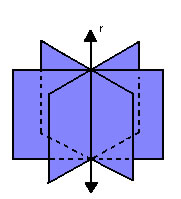 |
P8) Toda reta pertencente a um plano divide-o em duas regiões chamadas semiplanos.
P9) Qualquer plano divide o espaço em duas regiões chamadas semi-espaços.
Posições relativas de duas retas
No espaço, duas retas distintas podem ser concorrentes, paralelas ou reversas:
|
|
|
| Temos que considerar dois casos particulares: |
- retas perpendiculares:
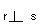
|
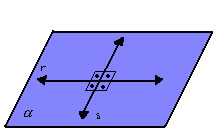 |
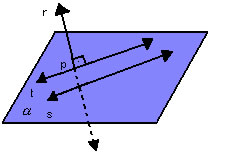
- retas ortogonais:
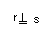
|
 |
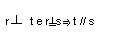 |
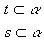 |
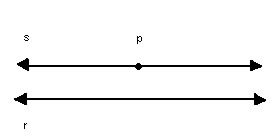
Postulado de Euclides ou das retas paralelas
P10) Dados uma reta r e um ponto P 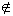 r, existe uma única reta s, traçada por P, tal que r // s: r, existe uma única reta s, traçada por P, tal que r // s: |
 |
 |
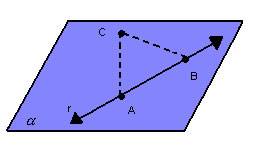
Determinação de um plano
Lembrando que, pelo postulado 5, um único plano passa por três pontos não-colineares, um plano também pode ser determinado por:
- uma reta e um ponto não-pertencente a essa reta:
|
 |
- duas retas distintas concorrentes:
|
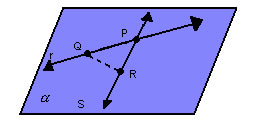 |
- duas retas paralelas distintas:
|
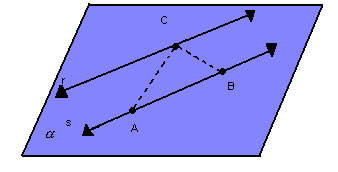 |
Posições relativas de reta e plano
Vamos considerar as seguintes situações:
a) reta contida no plano
Se uma reta r tem dois pontos distintos num plano  , então r está contida nesse plano: , então r está contida nesse plano: |
|
b) reta concorrente ou incidente ao plano
Dizemos que a reta r "fura" o plano  ou que r e ou que r e 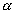 são concorrentes em P quando são concorrentes em P quando 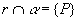 . . |
 |
Observação: A reta r é reversa a todas as retas do plano que não passam pelo ponto P.
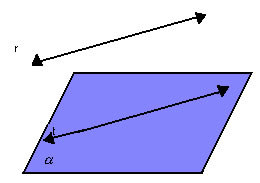
c) reta paralela ao plano
Se uma reta r e um plano 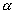 não têm ponto em comum, então a reta r é paralela a uma reta t contida no plano não têm ponto em comum, então a reta r é paralela a uma reta t contida no plano 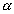 ; portanto, r // ; portanto, r // 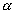
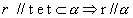
Em 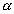 existem infinitas retas paralelas, reversas ou ortogonais a r. existem infinitas retas paralelas, reversas ou ortogonais a r. |
 |
P11) Se dois planos distintos têm um ponto em comum, então a sua intersecção é dada por uma única reta que passa por esse ponto. |
Perpendicularismo entre reta e plano
Uma reta r é perpendicular a um plano 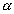 se, e somente se, r é perpendicular a todas as retas de se, e somente se, r é perpendicular a todas as retas de 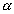 que passam pelo ponto de intersecção de r e que passam pelo ponto de intersecção de r e 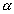 . . |
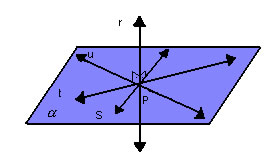 |
Note que:
- se uma reta r é perpendicular a um plano
 , então ela é perpendicular ou ortogonal a toda reta de , então ela é perpendicular ou ortogonal a toda reta de  : :
|
 |
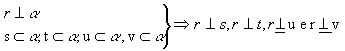 |
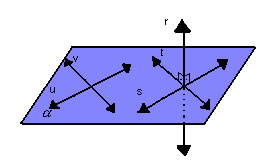
- para que uma reta r seja perpendicular a um plano
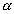 , basta ser perpendicular a duas retas concorrentes, contidas em , basta ser perpendicular a duas retas concorrentes, contidas em  : :
|
|
Observe, na figura abaixo, por que não basta que r seja perpendicular a uma única reta t de 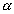 para que seja perpendicular ao plano: para que seja perpendicular ao plano: |
|
Posições relativas de dois planos
Consideramos as seguintes situações:
a) planos coincidentes ou iguais |
 |
b) planos concorrentes ou secantes |
|
c) planos paralelo
Dois planos, 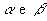 , são paralelos quando sua intersecção é vazia: , são paralelos quando sua intersecção é vazia: |
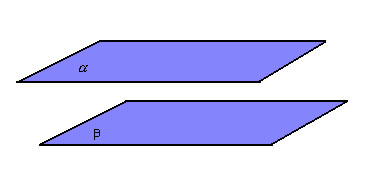 |
 |
Perpendicularismo entre planos
Dois planos, 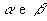 , são perpendiculares se, e somente se, existe uma reta de um deles que é perpendicular ao outro: , são perpendiculares se, e somente se, existe uma reta de um deles que é perpendicular ao outro: |
|
Observação: Existem infinitos planos perpendiculares a um plano dado; esses planos podem ser paralelos entre si ou secantes.
Projeção ortogonal
A projeção ortogonal de um ponto P sobre um plano 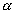 é a intersecção do plano com a reta perpendicular a ele, conduzida pelo ponto P: é a intersecção do plano com a reta perpendicular a ele, conduzida pelo ponto P: |
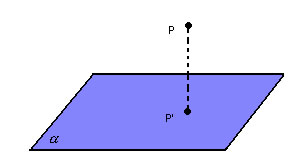 |
A projeção ortogonal de uma figura geométrica F ( qualquer conjunto de pontos) sobre um plano  é o conjunto das projeções ortogonais de todos os pontos de F sobre é o conjunto das projeções ortogonais de todos os pontos de F sobre  : : |
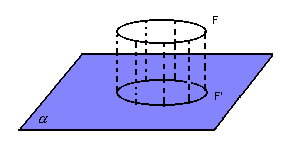 |
Distâncias |
A distância entre um ponto e um plano é a medida do segmento cujos extremos são o ponto e sua projeção ortogonal sobre o plano: |
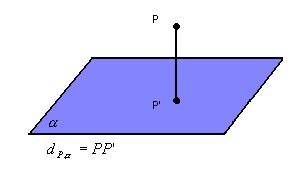
|
A distância entre uma reta e um plano paralelo é a distância entre um ponto qualquer da reta e o plano: |
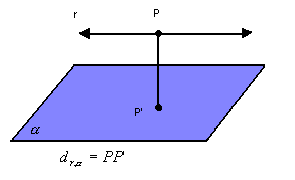
|
A distância entre dois planos paralelos é a distância entre um ponto qualquer de um deles e o outro plano: |
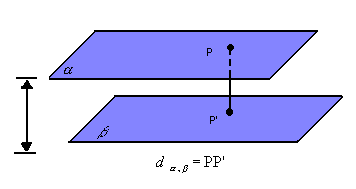
|
A distância entre duas retas reversas, r e s, é a distância entre um ponto qualquer de uma delas e o plano que passa pela outra e é paralelo à primeira reta: |
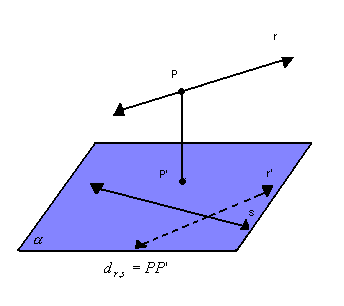
|
|
Ângulos |
O ângulo entre duas retas reversas é o ângulo agudo que uma delas forma com uma reta paralela à outra: |
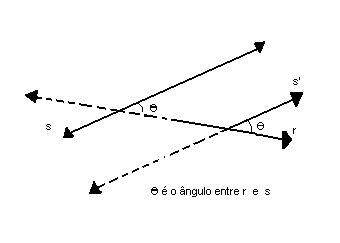
|
O ângulo entre uma reta e um plano é o ângulo que a reta forma com sua projeção ortogonal sobre o plano: |
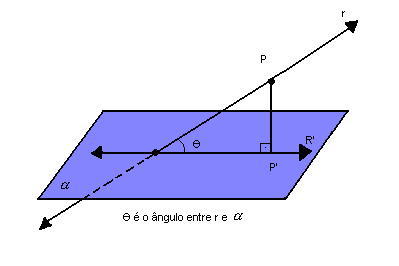
|
|
Observações:
 |
Diedros, triedos, poliedros
Diedros
Dois semiplanos não-coplanares, com origem numa mesma reta, determinam uma figura geométrica chamada ângulo diédrico, ou simplesmente diedro: |
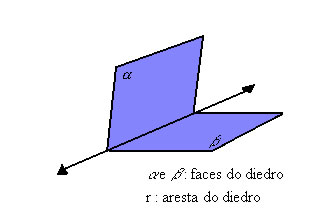 |
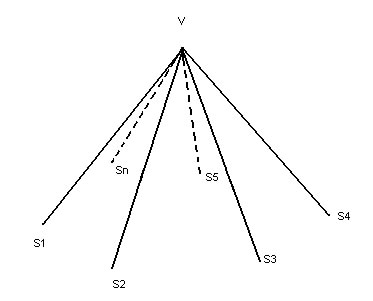
Triedos |
Três semi-retas não-coplanares, com origem num mesmo ponto, determinam três ângulos que formam uma figura geométrica chamada ângulo triédrico, ou simplesmente triedro: |
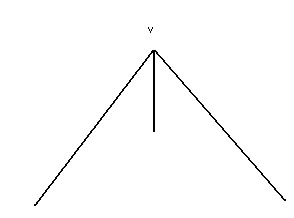 |
Ângulo poliédrico |
Sejam n 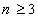 semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em que o plano de cada um deixa as outras semi-retas em um mesmo semi-espaço. A figura formada por esses ângulos é o ângulo poliédrico. semi-retas de mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas determinam n ângulos em que o plano de cada um deixa as outras semi-retas em um mesmo semi-espaço. A figura formada por esses ângulos é o ângulo poliédrico. |
 |
Poliedros
Chamamos de poliedro o sólido limitado por quatro ou mais polígonos planos, pertencentes a planos diferentes e que têm dois a dois somente uma aresta em comum. Veja alguns exemplos: |
|
Os polígonos são as faces do poliedro; os lados e os vértices dos polígonos são as arestas e os vértices do poliedro.
Poliedros convexos e côncavos
Observando os poliedros acima, podemos notar que, considerando qualquer uma de suas faces, os poliedros encontram-se inteiramente no mesmo semi-espaço que essa face determina. Assim, esses poliedros são denominados convexos.
Isso não acontece no último poliedro, pois, em relação a duas de suas faces, ele não está contido apenas em um semi-espaço. Portanto, ele é denominado côncavo.
Classificação
Os poliedros convexos possuem nomes especiais de acordo com o número de faces, como por exemplo:
- tetraedro: quatro faces
- pentaedro: cinco faces
- hexaedro: seis faces
- heptaedro: sete faces
- octaedro: oito faces
- icosaedro: vinte faces
|
Poliedros regulares
Um poliedro convexo é chamado de regular se suas faces são polígonos regulares, cada um com o mesmo número de lados e, para todo vértice, converge um mesmo número de arestas.
Existem cinco poliedros regulares: |
Poliedro |
Planificação |
Elementos |
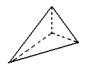
Tetraedro
|
|
4 faces triangulares
4 vértices
6 arestas |
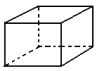
Hexaedro
|
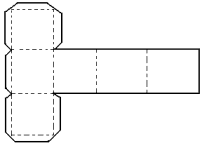
|
6 faces quadrangulares
8 vértices
12 arestas |
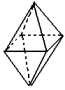
Octaedro
|
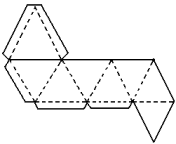
|
8 faces triangulares
6 vértices
12 arestas |
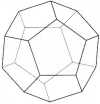
Dodecaedro
|
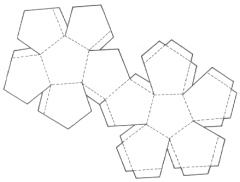
|
12 faces pentagonais
20 vértices
30 arestas |
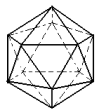
Icosaedro
|
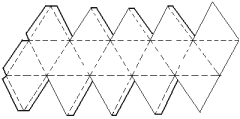
|
20 faces triangulares
12 vértices
30 arestas |
|
Relação de Euler
Em todo poliedro convexo é válida a relação seguinte:
V - A + F = 2
em que V é o número de vértices, A é o número de arestas e F, o número de faces.
Observe os exemplos: |
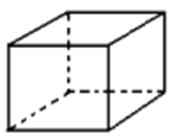
V=8 A=12 F=6
8 - 12 + 6 = 2
|
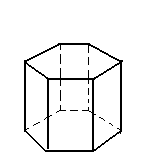
V = 12 A = 18 F = 8
12 - 18 + 8 = 2
|
|
Poliedros platônicos |
Diz-se que um poliedro é platônico se, e somente se:
a) for convexo;
b) em todo vértice concorrer o mesmo número de arestas;
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler.
Assim, nas figuras acima, o primeiro poliedro é platônico e o segundo, não-platônico.
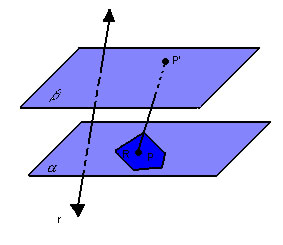
Prismas
Na figura abaixo, temos dois planos paralelos e distintos, 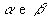 , um polígono convexo R contido em , um polígono convexo R contido em 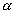 e uma reta r que intercepta e uma reta r que intercepta 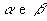 , mas não R: , mas não R: |
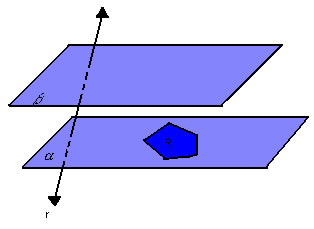 |
Para cada ponto P da região R, vamos considerar o segmento 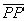 , paralelo à reta r , paralelo à reta r 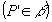 : : |
 |
Assim, temos: |
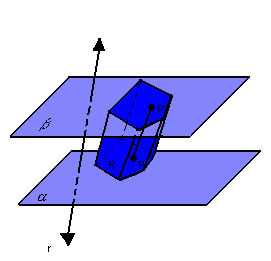 |
Chamamos de prisma ou prisma limitado o conjunto de todos os segmentos congruentes  paralelos a r. paralelos a r. |
Elementos do prisma
Dados o prisma a seguir, consideramos os seguintes elementos: |
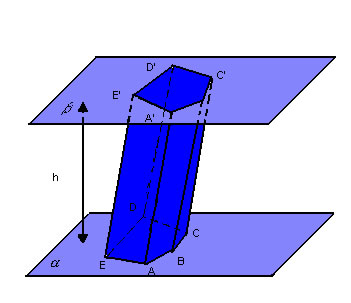 |
- bases:as regiões poligonais R e S
- altura:a distância h entre os planos
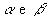
- arestas das bases:os lados
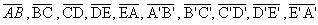 ( dos polígonos) ( dos polígonos)
- arestas laterais:os segmentos
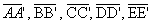
- faces laterais: os paralelogramos AA'BB', BB'C'C, CC'D'D, DD'E'E, EE'A'A
Classificação
Um prisma pode ser:
- reto: quando as arestas laterais são perpendiculares aos planos das bases;
- oblíquo: quando as arestas laterais são oblíquas aos planos das bases.
Veja: |
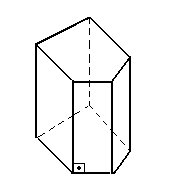
prisma reto
|
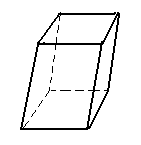
prisma oblíquo
|
Chamamos de prisma regular todo prisma reto cujas bases são polígonos regulares: |
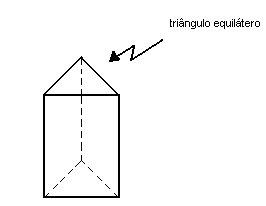
prisma regular triangular
|
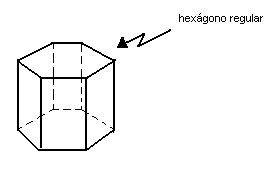
prisma regular hexagonal
|
|
| Observação: As faces de um prisma regular são retângulos congruentes. |
Secção |
Um plano que intercepte todas as arestas de um prisma determina nele uma região chamada secção do prisma.
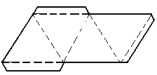
Secção transversal é uma região determinada pela intersecção do prisma com um plano paralelo aos planos das bases ( figura 1). Todas as secções transversais são congruentes ( figura 2). |
|
|
Áreas |
Num prisma, distinguimos dois tipos de superfície:as faces e as bases. Assim, temos de considerar as seguintes áreas:
a) área de uma face (AF ):área de um dos paralelogramos que constituem as faces;
b) área lateral ( AL ):soma das áreas dos paralelogramos que formam as faces do prisma.
No prisma regular, temos:
AL = n . AF (n = número de lados do polígono da base)
c) área da base (AB): área de um dos polígonos das bases;
d) área total ( AT): soma da área lateral com a área das bases
AT = AL + 2AB
Vejamos um exemplo.
Dado um prisma hexagonal regular de aresta da base a e aresta lateral h, temos: |
|
|
Paralelepípedo |
Todo prisma cujas bases são paralelogramos recebe o nome de paralelepípedo.Assim, podemos ter: |
a) paralelepípedo oblíquo
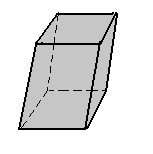 |
b) paralelepípedo reto
 |
|
Se o paralelepípedo reto tem bases retangulares, ele é chamado de paralelepípedo reto-retângulo,ortoedro ou paralelepípedo retângulo. |
| Paralelepípedo retângulo |
Seja o paralelepípedo retângulo de dimensões a, b e c da figura: |
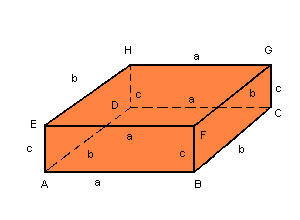 |
Temos quatro arestas de medida a, quatro arestas de medida b e quatro arestas de medida c; as arestas indicadas pela mesma letra são paralelas. |
Diagonais da base e do paralelepípedo |
| Considere a figura a seguir: |
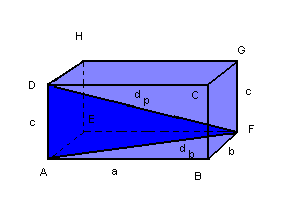
|
db = diagonal da base
dp = diagonal do paralelepípedo |
|
| Na base ABFE, temos: |
|
No triângulo AFD, temos: |
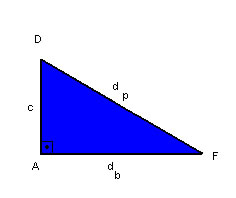 |
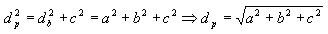 |
Área lateral |
| Sendo AL a área lateral de um paralelepípedo retângulo, temos: |
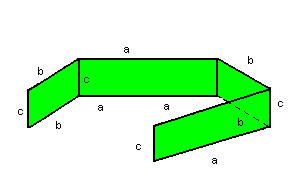 |
AL= ac + bc + ac + bc = 2ac + 2bc =AL = 2(ac + bc) |
| Área total |
Planificando o paralelepípedo, verificamos que a área total é a soma das áreas de cada par de faces opostas: |
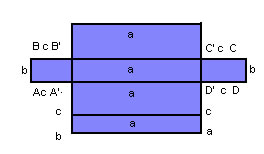 |
AT= 2( ab + ac + bc) |
Volume |
Por definição, unidade de volume é um cubo de aresta 1. Assim, considerando um paralelepípedo de dimensões 4, 2 e 2, podemos decompô-lo em 4 . 2 . 2 cubos de aresta 1: |
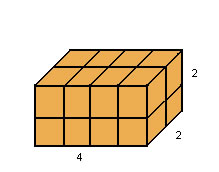 |
| Então, o volume de um paralelepípedo retângulo de dimensões a, b e c é dado por: V = abc |
Como o produto de duas dimensões resulta sempre na área de uma face e como qualquer face pode ser considerada como base, podemos dizer que o volume do paralelepípedo retângulo é o produto da área da base AB pela medida da altura h: |
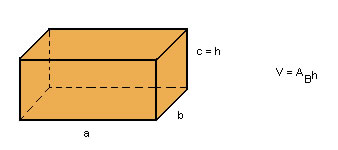 |
Cubo |
Um paralelepípedo retângulo com todas as arestas congruentes ( a= b = c) recebe o nome de cubo. Dessa forma, as seis faces são quadrados. |
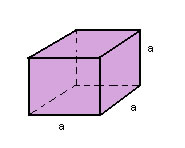
|
Diagonais da base e do cubo |
| Considere a figura a seguir: |
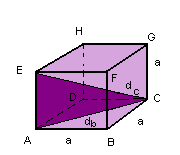
|
dc=diagonal do cubo
db = diagonal da base |
|
| Na base ABCD, temos: |
|
| No triângulo ACE, temos: |
|
Área lateral |
| A área lateral AL é dada pela área dos quadrados de lado a: |
|
Área total |
| A área total AT é dada pela área dos seis quadrados de lado a: |
|
| Volume |
De forma semelhante ao paralelepípedo retângulo, o volume de um cubo de aresta a é dado por:
V= a . a . a = a3 |
Generalização do volume de um prisma |
Para obter o volume de um prisma, vamos usar o princípio de Cavalieri ( matemático italiano, 1598 - 1697), que generaliza o conceito de volume para sólidos diversos.
Dados dois sólidos com mesma altura e um plano 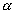 , se todo plano , se todo plano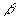 , paralelo a , paralelo a 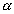 , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais: , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais: |
|
Se 1 é um paralelepípedo retângulo, então V2 = ABh.
Assim, o volume de todo prisma e de todo paralelepípedo é o produto da área da base pela medida da altura: |
|
Cilindro |
Na figura abaixo, temos dois planos paralelos e distintos,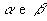 , um círculo R contido em , um círculo R contido em 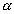 e uma reta r que intercepta e uma reta r que intercepta 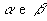 , mas não R: , mas não R: |
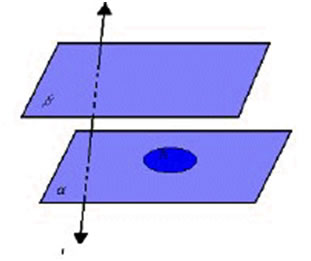 |
Para cada ponto C da região R, vamos considerar o segmento  , paralelo à reta r , paralelo à reta r 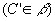 : : |
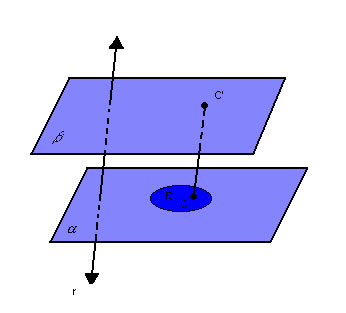 |
| Assim, temos: |
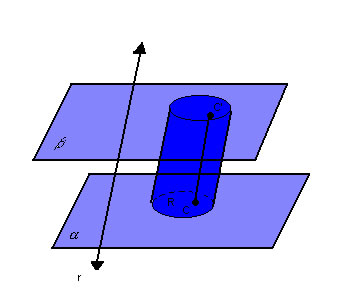 |
Chamamos de cilindro, ou cilindro circular, o conjunto de todos os segmentos  congruentes e paralelos a r. congruentes e paralelos a r.
|
Elementos do cilindro
Dado o cilindro a seguir, consideramos os seguintes elementos: |
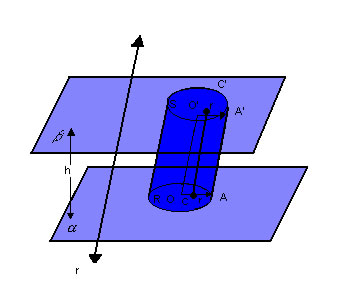 |
- bases: os círculos de centro O e O'e raios r
- altura: a distância h entre os planos
- geratriz: qualquer segmento de extremidades nos pontos das circunferências das bases ( por exemplo,
 ) e paralelo à reta r ) e paralelo à reta r
|
Classificação do Cilindro |
Um cilindro pode ser:
- circular oblíquo: quando as geratrizes são oblíquas às bases;
- circular reto: quando as geratrizes são perpendiculares às bases.
Veja:
|
|
O cilindro circular reto é também chamado de cilindro de revolução, por ser gerado pela rotação completa de um retângulo por um de seus lados. Assim, a rotação do retângulo ABCD pelo lado 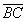 gera o cilindro a seguir: gera o cilindro a seguir: |
|
A reta 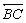 contém os centros das bases e é o eixo do cilindro. contém os centros das bases e é o eixo do cilindro.
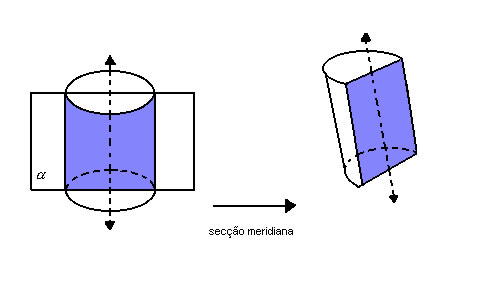
Secção
Secção transversal é a região determinada pela intersecção do cilindro com um plano paralelo às bases. Todas as secções transversais são congruentes. |
|
| Secção meridiana é a região determinada pela intersecção do cilindro com um plano que contém o eixo. |
 |
| Áreas |
Num cilindro, consideramos as seguintes áreas:
a) área lateral (AL)
Podemos observar a área lateral de um cilindro fazendo a sua planificação: |
|
Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões 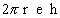 : :
b) área da base ( AB):área do círculo de raio r
c) área total ( AT): soma da área lateral com as áreas das bases
|
Volume |
Para obter o volume do cilindro, vamos usar novamente o princípio de Cavalieri.
Dados dois sólidos com mesma altura e um plano 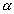 , se todo plano , se todo plano 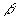 , paralelo ao plano , paralelo ao plano 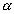 , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais: , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais: |
|
|
Se 1 é um paralelepípedo retângulo, então V2 = ABh.
Assim, o volume de todo paralelepípedo retângulo e de todo cilindro é o produto da área da base pela medida de sua altura:
No caso do cilindro circular reto, a área da base é a área do círculo de raio r 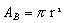 ; ;
portanto seu volume é: |
|
Cilindro eqüilátero |
Todo cilindro cuja secção meridiana é um quadrado ( altura igual ao diâmetro da base) é chamado cilindro eqüilátero. |
|
|
Cone circular |
Dado um círculo C, contido num plano 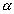 , e um ponto V ( vértice) fora de , e um ponto V ( vértice) fora de 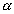 , chamamos de cone circular o conjunto de todos os segmentos , chamamos de cone circular o conjunto de todos os segmentos 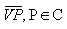 |
|
Elementos do cone circular
Dado o cone a seguir, consideramos os seguintes elementos: |
|
- altura: distância h do vértice V ao plano
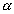
- geratriz (g):segmento com uma extremidade no ponto V e outra num ponto da circunferência
- raio da base: raio R do círculo
- eixo de rotação:reta
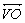 determinada pelo centro do círculo e pelo vértice do cone determinada pelo centro do círculo e pelo vértice do cone
|
Cone reto |
Todo cone cujo eixo de rotação é perpendicular à base é chamado cone reto, também denominado cone de revolução. Ele pode ser gerado pela rotação completa de um triângulo retângulo em torno de um de seus catetos. |
|
|
Da figura, e pelo Teorema de Pitágoras, temos a seguinte relação:
Secção meridiana
A secção determinada, num cone de revolução, por um plano que contém o eixo de rotação é chamada secção meridiana. |
|
Se o triângulo AVB for eqüilátero, o cone também será eqüilátero: |
|
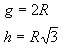 |
Áreas |
Desenvolvendo a superfície lateral de um cone circular reto, obtemos um setor circular de raio g e comprimento 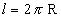 : : |
|
| Assim, temos de considerar as seguintes áreas: |
a) área lateral (AL): área do setor circular |
|
b) área da base (AB):área do circulo do raio R |
|
c) área total (AT):soma da área lateral com a área da base |
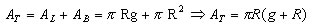 |
Volume |
| Para determinar o volume do cone, vamos ver como calcular volumes de sólidos de revolução. Observe a figura: |
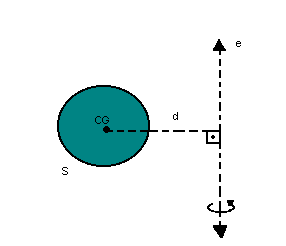
|
d = distância do centro de gravidade (CG) da sua superfície ao eixo e
S=área da superfície |
|
Sabemos, pelo Teorema de Pappus - Guldin, que, quando uma superfície gira em torno de um eixo e, gera um volume tal que:
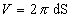
Vamos, então, determinar o volume do cone de revolução gerado pela rotação de um triângulo retângulo em torno do cateto h: |
|
O CG do triângulo está a uma distância 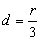 do eixo de rotação. Logo: do eixo de rotação. Logo:
 |
Pirâmides |
Dados um polígono convexo R, contido em um plano  , e um ponto V ( vértice) fora de , e um ponto V ( vértice) fora de  , chamamos de pirâmide o conjunto de todos os segmentos , chamamos de pirâmide o conjunto de todos os segmentos 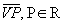 . . |
|
Elementos da pirâmide
Dada a pirâmide a seguir, temos os seguintes elementos: |
|
- base: o polígono convexo R
- arestas da base: os lados
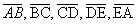 do polígono do polígono
- arestas laterais: os segmentos
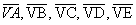
- faces laterais: os triângulos VAB, VBC, VCD, VDE, VEA
- altura: distância h do ponto V ao plano
|
Classificação |
Uma pirâmide é reta quando a projeção ortogonal do vértice coincide com o centro do polígono da base.
Toda pirâmide reta, cujo polígono da base é regular, recebe o nome de pirâmide regular. Ela pode ser triangular, quadrangular, pentagonal etc., conforme sua base seja, respectivamente, um triângulo, um quadrilátero, um pentágono etc.
Veja: |
|
|
Observações:
1ª) Toda pirâmide triangular recebe o nome do tetraedro. Quando o tetraedro possui como faces triângulos eqüiláteros, ele é denominado regular ( todas as faces e todas as arestas são congruentes). |
|
2ª) A reunião, base com base, de duas pirâmides regulares de bases quadradas resulta num octaedro. Quando as faces das pirâmides são triângulos eqüiláteros, o octaedro é regular.
|
Secção paralela à base de uma pirâmide |
Um plano paralelo à base que intercepte todas as arestas laterais determina uma secção poligonal de modo que:
- as arestas laterais e a altura sejam divididas na mesma razão;
- a secção obtida e a base sejam polígonos semelhantes;
- as áreas desses polígonos estejam entre si assim como os quadrados de suas distâncias ao vértice.
|
|
|
Relações entre os elementos de uma pirâmide regular |
| Vamos considerar uma pirâmide regular hexagonal, de aresta lateral l e aresta da base a: |
|
Assim, temos:
- A base da pirâmide é um polígono regular inscritível em um círculo de raio OB = R.
|
|
- A face lateral da pirâmide é um triângulo isósceles.
|
|
- Os triângulos VOB e VOM são retângulos.
|
|
Áreas |
Numa pirâmide, temos as seguintes áreas:
a) área lateral ( AL): reunião das áreas das faces laterais
b) área da base ( AB): área do polígono convexo ( base da pirâmide)
c) área total (AT): união da área lateral com a área da base
AT = AL +AB
Para uma pirâmide regular, temos:
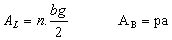
em que:
|
 |
Volume |
O princípio de Cavalieri assegura que um cone e uma pirâmide equivalentes possuem volumes iguais: |
|
Troncos |
Se um plano interceptar todas as arestas de uma pirâmide ou de um cone, paralelamente às suas bases, o plano dividirá cada um desses sólidos em dois outros: uma nova pirâmide e um tronco de pirâmide; e um novo cone e um tronco de cone.
Vamos estudar os troncos.
Tronco da pirâmide
Dado o tronco de pirâmide regular a seguir, temos:
|
|
- as bases são polígonos regulares paralelos e semelhantes;
- as faces laterais são trapézios isósceles congruentes.
|
Áreas |
Temos as seguintes áreas:
a) área lateral (AL): soma das áreas dos trapézios isósceles congruentes que formam as faces laterais
b) área total (AT): soma da área lateral com a soma das áreas da base menor (Ab) e maior (AB) |
|
Volume |
O volume de um tronco de pirâmide regular é dado por:
|
Sendo V o volume da pirâmide e V' o volume da pirâmide obtido pela secção é válida a relação:
|
Tronco do cone |
Sendo o tronco do cone circular regular a seguir, temos: |
|
- as bases maior e menor são paralelas;
- a altura do tronco é dada pela distância entre os planos que contém as bases.
|
Áreas
Temos:
a) área lateral |
|
b) área total
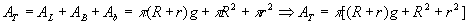 |
Volume |
|
Sendo V o volume do cone e V' o volume do cone obtido pela secção são válidas as relações:
Esfera
Chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R.
Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior. |
|
Volume
O volume da esfera de raio R é dado por:
Partes da esfera
Superfície esférica
A superfície esférica de centro O e raio R é o conjunto de pontos do es[aço cuja distância ao ponto O é igual ao raio R.
Se considerarmos a rotação completa de uma semicircunferência em torno de seu diâmetro, a superfície esférica é o resultado dessa rotação. |
|
A área da superfície esférica é dada por:
|
| Zona esférica |
| É a parte da esfera gerada do seguinte modo: |
|
A área da zona esférica é dada por:
Calota esférica
É a parte da esfera gerada do seguinte modo: |
|
Ä área da calota esférica é dada por:
Fuso esférico
O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semi-circunferência de um ângulo 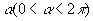 em torno de seu eixo: em torno de seu eixo: |
|
A área do fuso esférico pode ser obtida por uma regra de três simples: |
|
Cunha esférica
Parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo 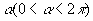 : : |
|
O volume da cunha pode ser obtido por uma regra de três simples: |
|
| |
| |
| |
| |
| |
| |
| |
| |
|
| |
| |
| |
|
|